其中  为函数
为函数 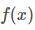 的梯度向量,
的梯度向量,  为函数
为函数 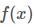 的Hesse(Hessian)矩阵。
的Hesse(Hessian)矩阵。
上述牛顿法不是全局收敛的。为此可以引入阻尼牛顿法(又称带步长的牛顿法)。
我们知道,求极值的一般迭代格式为
其中  为搜索步长,
为搜索步长,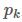 为搜索方向(注意所有的迭代格式都是先计算搜索方向,再计算搜索步长,如同瞎子下山一样,先找到哪个方向可行下降,再决定下几步)。
为搜索方向(注意所有的迭代格式都是先计算搜索方向,再计算搜索步长,如同瞎子下山一样,先找到哪个方向可行下降,再决定下几步)。
取下降方向  即得阻尼牛顿法,只不过搜索步长
即得阻尼牛顿法,只不过搜索步长 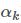 不确定,需要用线性搜索技术确定一个较优的值,比如精确线性搜索或者Goldstein搜索、Wolfe搜索等。特别地,当
不确定,需要用线性搜索技术确定一个较优的值,比如精确线性搜索或者Goldstein搜索、Wolfe搜索等。特别地,当  一直取为常数1时,就是普通的牛顿法。
一直取为常数1时,就是普通的牛顿法。
以Rosenbrock函数为例,即有
于是可得函数的梯度
编写Python代码如下(使用版本为Python3.3):
"""
Newton法
Rosenbrock函数
函数 f(x)=100*(x(2)-x(1).^2).^2+(1-x(1)).^2
梯度 g(x)=(-400*(x(2)-x(1)^2)*x(1)-2*(1-x(1)),200*(x(2)-x(1)^2))^(T)
"""
import numpy as np
import matplotlib.pyplot as plt
def jacobian(x):
return np.array([-400*x[0]*(x[1]-x[0]**2)-2*(1-x[0]),200*(x[1]-x[0]**2)])
def hessian(x):
return np.array([[-400*(x[1]-3*x[0]**2)+2,-400*x[0]],[-400*x[0],200]])
X1=np.arange(-1.5,1.5+0.05,0.05)
X2=np.arange(-3.5,2+0.05,0.05)
[x1,x2]=np.meshgrid(X1,X2)
f=100*(x2-x1**2)**2+(1-x1)**2; # 给定的函数
plt.contour(x1,x2,f,20) # 画出函数的20条轮廓线
def newton(x0):
print('初始点为:')
print(x0,'\n')
W=np.zeros((2,10**3))
i = 1
imax = 1000
W[:,0] = x0
x = x0
delta = 1
alpha = 1
while i<imax and delta>10**(-5):
p = -np.dot(np.linalg.inv(hessian(x)),jacobian(x))
x0 = x
x = x + alpha*p
W[:,i] = x
delta = sum((x-x0)**2)
print('第',i,'次迭代结果:')
print(x,'\n')
i=i+1
W=W[:,0:i] # 记录迭代点
return W
x0 = np.array([-1.2,1])
W=newton(x0)
plt.plot(W[0,:],W[1,:],'g*',W[0,:],W[1,:]) # 画出迭代点收敛的轨迹
plt.show()
上述代码中jacobian(x)返回函数的梯度,hessian(x)返回函数的Hesse矩阵,用W矩阵记录迭代点的坐标,然后画出点的搜索轨迹。
可得输出结果为
初始点为: [-1.2 1. ] 第 1 次迭代结果: [-1.1752809 1.38067416] 第 2 次迭代结果: [ 0.76311487 -3.17503385] 第 3 次迭代结果: [ 0.76342968 0.58282478] 第 4 次迭代结果: [ 0.99999531 0.94402732] 第 5 次迭代结果: [ 0.9999957 0.99999139] 第 6 次迭代结果: [ 1. 1.]
即迭代了6次得到了最优解,画出的迭代点的轨迹如下:
由于主要使用了Python的Numpy模块来进行计算,可以看出,代码和最终的图与Matlab是很相像的。
以上这篇使用Python实现牛顿法求极值就是小编分享给大家的全部内容了,希望能给大家一个参考,也希望大家多多支持。
免责声明:本站资源来自互联网收集,仅供用于学习和交流,请遵循相关法律法规,本站一切资源不代表本站立场,如有侵权、后门、不妥请联系本站删除!
《魔兽世界》大逃杀!60人新游玩模式《强袭风暴》3月21日上线
暴雪近日发布了《魔兽世界》10.2.6 更新内容,新游玩模式《强袭风暴》即将于3月21 日在亚服上线,届时玩家将前往阿拉希高地展开一场 60 人大逃杀对战。
艾泽拉斯的冒险者已经征服了艾泽拉斯的大地及遥远的彼岸。他们在对抗世界上最致命的敌人时展现出过人的手腕,并且成功阻止终结宇宙等级的威胁。当他们在为即将于《魔兽世界》资料片《地心之战》中来袭的萨拉塔斯势力做战斗准备时,他们还需要在熟悉的阿拉希高地面对一个全新的敌人──那就是彼此。在《巨龙崛起》10.2.6 更新的《强袭风暴》中,玩家将会进入一个全新的海盗主题大逃杀式限时活动,其中包含极高的风险和史诗级的奖励。
《强袭风暴》不是普通的战场,作为一个独立于主游戏之外的活动,玩家可以用大逃杀的风格来体验《魔兽世界》,不分职业、不分装备(除了你在赛局中捡到的),光是技巧和战略的强弱之分就能决定出谁才是能坚持到最后的赢家。本次活动将会开放单人和双人模式,玩家在加入海盗主题的预赛大厅区域前,可以从强袭风暴角色画面新增好友。游玩游戏将可以累计名望轨迹,《巨龙崛起》和《魔兽世界:巫妖王之怒 经典版》的玩家都可以获得奖励。
更新日志
- 凤飞飞《我们的主题曲》飞跃制作[正版原抓WAV+CUE]
- 刘嘉亮《亮情歌2》[WAV+CUE][1G]
- 红馆40·谭咏麟《歌者恋歌浓情30年演唱会》3CD[低速原抓WAV+CUE][1.8G]
- 刘纬武《睡眠宝宝竖琴童谣 吉卜力工作室 白噪音安抚》[320K/MP3][193.25MB]
- 【轻音乐】曼托凡尼乐团《精选辑》2CD.1998[FLAC+CUE整轨]
- 邝美云《心中有爱》1989年香港DMIJP版1MTO东芝首版[WAV+CUE]
- 群星《情叹-发烧女声DSD》天籁女声发烧碟[WAV+CUE]
- 刘纬武《睡眠宝宝竖琴童谣 吉卜力工作室 白噪音安抚》[FLAC/分轨][748.03MB]
- 理想混蛋《Origin Sessions》[320K/MP3][37.47MB]
- 公馆青少年《我其实一点都不酷》[320K/MP3][78.78MB]
- 群星《情叹-发烧男声DSD》最值得珍藏的完美男声[WAV+CUE]
- 群星《国韵飘香·贵妃醉酒HQCD黑胶王》2CD[WAV]
- 卫兰《DAUGHTER》【低速原抓WAV+CUE】
- 公馆青少年《我其实一点都不酷》[FLAC/分轨][398.22MB]
- ZWEI《迟暮的花 (Explicit)》[320K/MP3][57.16MB]








