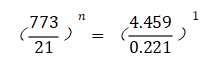《原神》中的剧变反应主要是改动了公式。比之前强了,然后是游戏中角色的基础剧变反应伤害提升了20%。精通的收益相较于改版之前提升了67%。剧变反应伤害提升百分百。之后剧变反应队伍可以尝试搞一下。
剧变反应改动详解
(即原公式)结晶、增幅公式:
SP=k*(25*EM)/(9*(1400+EM))
EM为元素精通,SP为精通对反应伤害提升的百分比
Part 1 —— 精通收益推导过程
问题产生:
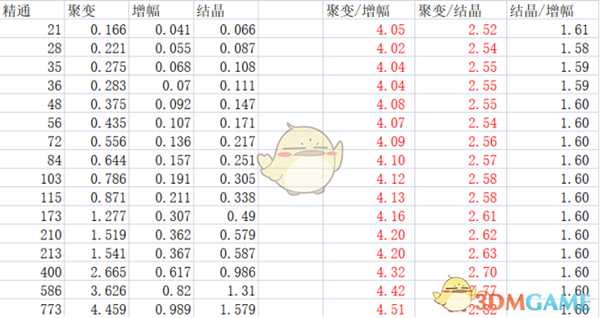
记录了新版本“详细面板”中给出的一组数据,从16到773精通,取点,因为装备有限,只能取到那么多样本了。
然后将数据写入exl中,分别用【精通对于聚变的加成】(以下简称“聚变”)除以【增幅】(同样简称)、聚变/结晶、结晶/增幅。
发现结晶和增幅之间存在稳定的比例关系,比例系数1.6。
但聚变和另外两种反应的收益情况明显不成固定的比例关系。
这说明,老公式肯定不能用了,聚变反应肯定存在一个新的精通关系式。
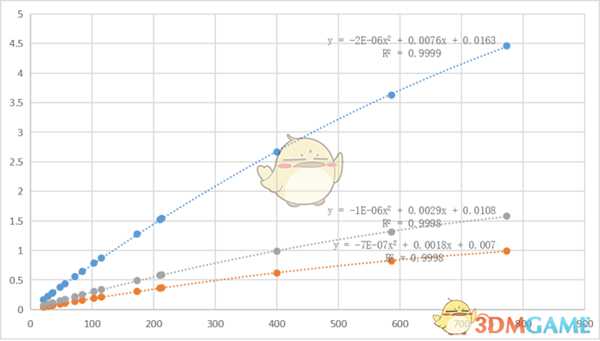
接下来,把数据用点阵图来呈现,并用exl的多项式拟合初步给出趋势图像:
根据图中的趋势,结合直觉猜想,这是一个单调递增,导数单调减的函数,而且我一开始觉得这个函数应该是发散的,不存在极限。
目前可选函数有:多项式、根式函数、反比例函数、对数、对数与多项式复合
我首先排除了多项式函数,因为多项式函数如果要做到上图中的效果,必然在后方会出现最大值,而经过最大值就意味着函数变为递减,这是不可能的,游戏里怎么可能堆高了属性会负收益?
接下来我对根式函数进行了尝试,如果这个函数是与x小于1的次方成正比的,那么可以从头尾两个数值粗略计算出一个幂值
最终得到n约为0.9
但代入了中间的几个值发现,误差很大,我果断放弃了这种思路。
然后我去尝试了更有希望的对数函数,因为我一直觉得反比例函数是收敛的所以不太可能,先看看对数函数的情况。
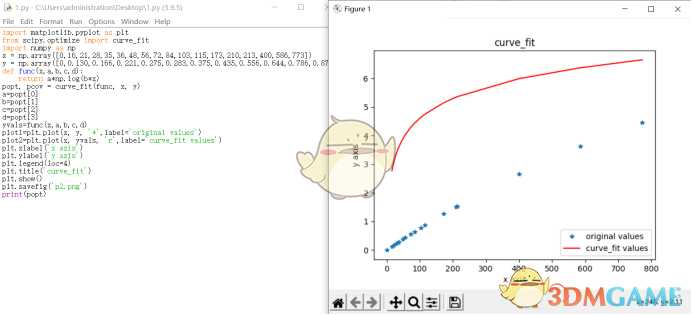
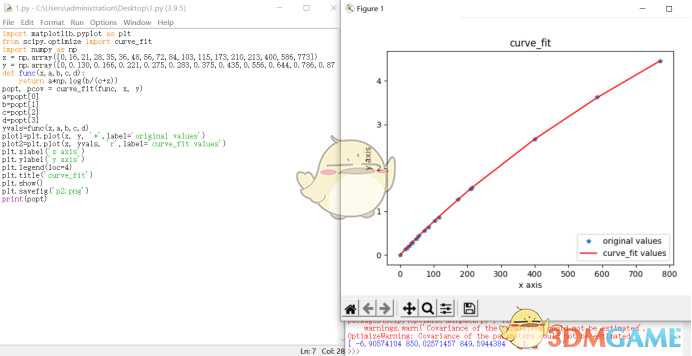
当场请教学习了一波Python拟合
一开始我直接用对数函数,发现这图像直接飞起来,必须用复合函数进行处理,几番尝试以后发现了一个比较好的解:
得到的公式约为:
SP=-6.9ln(850/(EM+850))
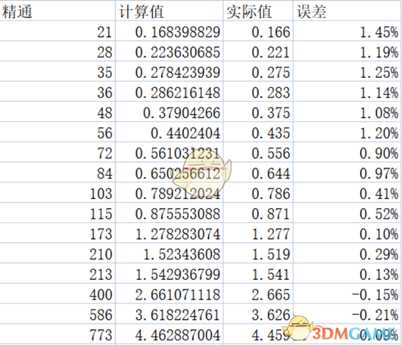
得到了这样的误差情况,已经算不错了,我原本就准备用这个公式作为结论了,毕竟对数函数是不收敛的比较符合直觉(x在分母上只要前边系数提出-1就到分子上了),然后我顺便尝试了一下老公式反比例函数的格式拟合:
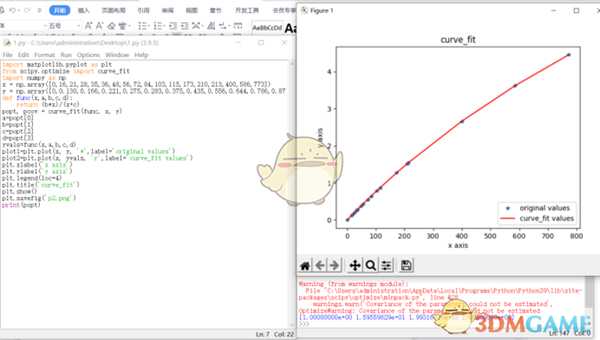
发现这个也能得到一个契合度非常高的公式,
SP=(16*EM)/(EM+2000)
我再将其代入exl中进行误差分析:
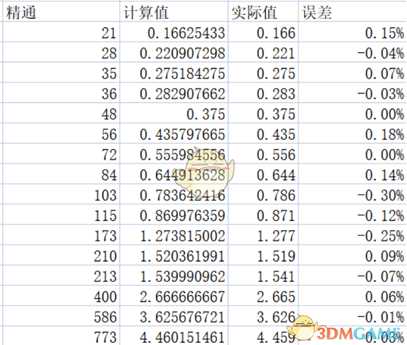
相比之前的对数函数,误差竟然直接少了一个数量级!
毫无疑问,肯定要选这个函数作为结论了,而且精度非常高,取三位小数后基本就是和实际值一模一样,肯定符合使用需求了。
到此,我便成功得到了一个精度非常高的经验公式:
SP=(16*EM)/(EM+2000)
而且,最终结果仍然是反比例函数,最大值为16,也就是1600%聚变加成,根本不可能达到,不可能影响游戏,虽然是收敛的,但其实也算比较合理了。
免责声明:本站资源来自互联网收集,仅供用于学习和交流,请遵循相关法律法规,本站一切资源不代表本站立场,如有侵权、后门、不妥请联系本站删除!
更新日志
- 凤飞飞《我们的主题曲》飞跃制作[正版原抓WAV+CUE]
- 刘嘉亮《亮情歌2》[WAV+CUE][1G]
- 红馆40·谭咏麟《歌者恋歌浓情30年演唱会》3CD[低速原抓WAV+CUE][1.8G]
- 刘纬武《睡眠宝宝竖琴童谣 吉卜力工作室 白噪音安抚》[320K/MP3][193.25MB]
- 【轻音乐】曼托凡尼乐团《精选辑》2CD.1998[FLAC+CUE整轨]
- 邝美云《心中有爱》1989年香港DMIJP版1MTO东芝首版[WAV+CUE]
- 群星《情叹-发烧女声DSD》天籁女声发烧碟[WAV+CUE]
- 刘纬武《睡眠宝宝竖琴童谣 吉卜力工作室 白噪音安抚》[FLAC/分轨][748.03MB]
- 理想混蛋《Origin Sessions》[320K/MP3][37.47MB]
- 公馆青少年《我其实一点都不酷》[320K/MP3][78.78MB]
- 群星《情叹-发烧男声DSD》最值得珍藏的完美男声[WAV+CUE]
- 群星《国韵飘香·贵妃醉酒HQCD黑胶王》2CD[WAV]
- 卫兰《DAUGHTER》【低速原抓WAV+CUE】
- 公馆青少年《我其实一点都不酷》[FLAC/分轨][398.22MB]
- ZWEI《迟暮的花 (Explicit)》[320K/MP3][57.16MB]